Si vous souhaitez réaliser un travail nécessitant un angle droit, sans avoir d’équerre sous la main, une erreur de visée peut passer inaperçue si la réalisation est de petite dimension.
Il en est tout autrement s’il s’agit, par exemple, de réaliser deux cloisons perpendiculaires l’une avec l’autre.
Alors, comment faire ?
Si en replongeant dans vos lointains souvenirs d’école, Pythagore vous dit quelque chose, c’est parfait, car la solution vient de là.
Sinon, voici ce que nous dit le théorème de Pythagore :
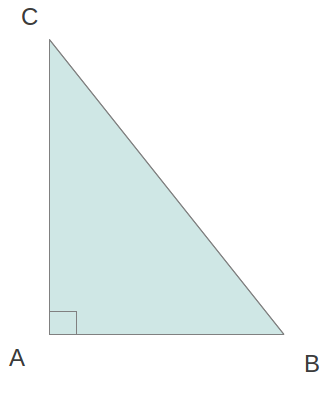
(BC)² = (AB)² + (AC)²
Heu… si tu crois qu’on va avoir envie de se cogner des maths pendant le bricolage…
Oui, croyez-bien que ce n’est pas le but recherché.
Et heureusement, il y a beaucoup plus simple pour appliquer ce théorème, sans faire de calcul et en plus très rapidement.
La méthode pour se rappeler de cette formule, c’est 3 – 4 – 5 !
(3)² + (4)² = (5)² => 9 + 16 = 25
Vous pouvez donc en déduire des longueurs personnalisées comme 30 cm – 40 cm – 50 cm
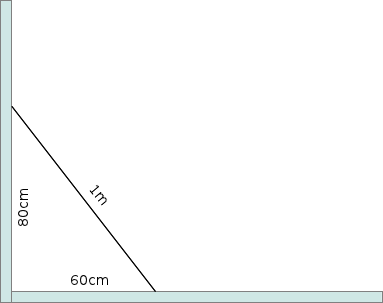
Il y a aussi 60 cm – 80 cm – 1m.
Ainsi, pour un côté d’une cloison de 60 cm et 80 cm sur l’autre cloison, si ces deux cloisons sont perpendiculaires l’une avec l’autre, vous aurez exactement 1m entre ces deux points comme illustré ci-dessous :
Si vous n’avez pas 1m, c’est que vos cloisons ne forment pas un parfait angle droit !
Plus les longueurs de mesures sont grandes, meilleure sera la précision !










je veux faire mon beton pour ma dalle de 8metres carre a la betonniere
combien de sac de ciment combien de sable et je suis en pleine montagen des gravats et des caillouis j’en ai merçi de me renseigner.
Bonsoir Fernand,
Pardon pour le délai à vous répondre, j’étais absent pour cause de vacances.
Là, vous me posez une colle, car je prends toujours mon béton ou mon mortier tout fait directement à la centrale béton la plus proche du chantier.
La quantité de ciment varie suivant la dureté que l’on souhaite obtenir, mais je dirais qu’il faut en moyenne 1 seau de ciment pour 4 de sable et 1 de cailloux.
Donc, en fonction de ces moyennes, une fois votre volume total calculé pour la dalle, vous divisez ce volume par 5 (4 pour le sable + 1 pour les cailloux), et vous aurez une idée de ce qu’il vous faut en sable et en cailloux. Prévoyez un peu plus, on ne sait jamais 😉 !
Dans un sac de ciment de 35kg, il doit y avoir environ 3 ou 4 seaux de ciment.
Re-dites-moi si mon estimation est bonne… ou pas 😉 !
Bien amicalement
Christophe
sur le principe, petit truc de vieux maçon :
Une ficelle circulaire de longueur multiple de 12 (3 carré + 4 carré = 5 carré) avec 12 noeuds équidistants.
je fixe une longueur de 3 noeuds sur le premier madrier, une de 4 noeuds sur le deuxiéme. Quand la longueur de 5 noeuds est tendu, c’est que mon angle est droit.
Bonjour,
Formule du béton armé dosé à 350 kg de ciment par mètre cube :
Poids Volume
70 kg de ciment 33 litres
160 kg de sable 100 litres
260 kg de gravier 160 litres
34 kg d’eau 34 litres
524 kg au total ou 200 litres*
Soit 3 pelles de ciment, 9 pelles de sable, 14,5 pelle de gravier, 9,25 litres d’eau (à raison de 3 litres par pelle, 10 litres par seaux**)
* Le volume final ne correspond pas à la somme des volumes de chaque élément parce que l’ensemble se compacte. Le sable remplit les interstices du gravier, le ciment remplit les interstices du sable et l’eau compacte l’ensemble.
** Vous pouvez désormais modifier la contenance d’une pelle. Par défaut et par expérience, la contenance d’une pelle est fixée à 3 litres. Pour vous faire une idée assez précise, faites quelques essais avec du sable, une pelle et un seau de 10 litres, puis compter le nombre de pelles pour remplir le seau à ras bord. Divisez le volume du seau (10 litres) par le nombre de pelles de sable et vous obtenez la contenance moyenne d’une pelle.
La quantité d’eau peut varier en fonction de l’humidité du sable. Dans la majorité des cas, les maçons dosent l’eau au feeling de façon à obtenir une consistance pâteuse du mélange.
Contrairement à une idée répandue, l’eau ne s’évapore que très peu. Elle sert à la réaction chimique qui se produit lors du durcissement. L’évaporation lors du séchage est néfaste puisqu’elle réduit la proportion d’eau entrant en réaction avec le ciment, ce qui génère des fissures. Pour cette raison il est préférable de couler du béton par temps froid (mais supérieur à 0° Celsius) ou humide.
Merci pour l’aide. Je fais de la maçonnerie a montréal et je cherche toujours de bons astuces.