Quand on réalise soi-même son projet en ossature bois (garage, carport, extension, etc.), on se heurte très rapidement à cette question concernant la pente de toiture :
Quel est l’angle auquel je dois couper le haut de mes bastaings verticaux pour avoir un assemblage parfait ?
Je dois préciser qu’il s’agit ici d’une faible pente et d’une toiture en bac acier ou en polycarbonate.
Quelques illustrations seraient sûrement plus parlantes pour illustrer mes propos 😉 .
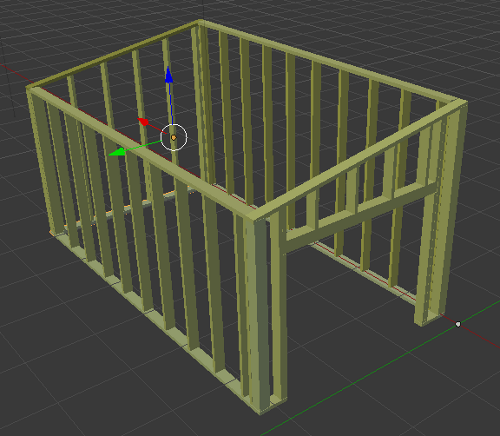
Voici une réalisation en ossature bois (avant la pose de la toiture) :
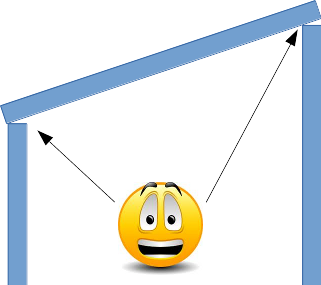
Si on regarde les côtés, on ne peut avoir un assemblage des bastaings comme cela :
Mais bien de cette façon :
Il existe différentes méthodes plus ou moins efficaces mais souvent longues et laborieuses à mettre en pratique pour connaître l’angle de coupe.
Par exemple, on peut tendre une ficelle entre les deux bastaings et relever l’angle à l’aide d’une fausse équerre.
Mais pour pouvoir effectuer un tel relevé, il faut que les bastaings soient déjà fixés !
Or, on veut d’abord les couper avant de les fixer !
Il est donc impératif de connaître l’angle de coupe.
Je vous propose donc ma technique, simple, hyper rapide (moins de 3 minutes) et d’une précision redoutable, comme vous pourrez en juger sur la photo finale.
Pour lire la suite, vous devez être abonné.
Abonnez-vous dès maintenant !
Cliquez ici si vous avez perdu votre mot de passe
Vous ne souhaitez pas vous abonner ?
Vous pouvez quand même lire l’intégralité de cet article
en sélectionnant ci-dessous un mode de micro-paiement
(Une fois le micro-paiement effectué, l’intégralité de l’article est automatiquement affiché)
|
Vous avez aimé cet article ? Lisez La Totalité Des Articles
pour Seulement 2 € par mois ! (Sans engagement) + Vous avez un accès complet aux articles protégés, aux formations et projets réservés exclusivement aux membres. + Votre fidélité est récompensée (remises cumulables jusqu'à 50%) à valoir sur tous les dossiers existants et à paraître + Et pleins d'autres surprises...
|










Bonsoir
Merci pour les nombreux articles qui sont toujours top top..
y aura t il des articles sur les odeurs des syphons par manque de pente
??? Biensur en evitant de tout casser …
bonne continuation .
Merci pour tous vos articles et conseils très percutants.
J’ai découvert grâce à vous la sous-couche WEBER à mettre avant de poser le
carrelage dans une douche à l’italienne.
Pour info ce produit se trouve dans les magasins LAPEYRE.
Pour ce qui est de la protection des joints de carrelage, je n’ai pas trouvé le
produit. Pouvez-vous me dire où se le procurer.
Peut-on faire un béton ciré sur la sous-couche WEBER ?
Connaissez-vous le vendeur MAISON ETANCHE, peut-on acheter sur le site du béton ?
Merci pour vos réponses.
Cordialement.
J’aurais eu ses infos avant, cela m’aurais éviter des calculs d’apothicaires, cordelette tendue entre 2 bastaing et maintenu par 4 etais metsapro. Imagine le montage pour avoir un relevé de toutes les hauteurs à chaques montants. Finalament moins de 2mm de diff sur 16m de façades, pas trop mâl !
Un grand merci pour tes super conseils qui serviront à tous ceux qui n’ont pas encore commencé leurs réalisations.
Bonjour,
Pour ne pas avoir à refaire tout le schéma à l’échelle réduite sur du papier, vous pouvez aussi utiliser une calculatrice, encore plus simple 😉
il suffit de retrancher la hauteur du bastaing vertical long à la hauteur du bastaing vertical court (ici, 250-230 = 20).
De diviser cette valeur par la largeur entre les bastaing (260 ici).
on obtient 20/260.
De prendre une calculatrice et d’utiliser la fonction Arc tangente de cette valeur (c’est à dire l’arc dont la tangente vaut 20/260 (la tangente est le rapport coté opposé/coté adjacent d’un triangle rectangle).
Cette fonction est couramment notée tan-1 et on la retrouve sur toutes les calculatrices, notamment celle d’un téléphone par exemple ;)(ou la calculatrice windows)).
Dans l’exemple en question, on obtient un angle de 4.4°, que l’on peut reporter sur son outillage 😉
Voila pour ma première « petite » pierre à l’édifice et merci pour ce super site je découvre seulement aujourd’hui.
A+
Bonsoir Anthony,
Merci pour votre référence à la trigo à laquelle je n’ai malheureusement jamais rien compris !
Votre explication me donne cependant envie de comprendre car cela peut être drôlement intéressant dans certaines situations. (C’est un peu comme le théorème de Pythagore que j’utilise souvent et qui ne me pose pas de problème de compréhension).
Donc j’essaie votre formule dans excel en tapant la formule suivante : +TAN(20/260) ce qui donne un résultat de 0,07707516 !
Comment faut-il faire pour obtenir un résultat en degré ?
Merci pour votre éclaircissement.
Cordialement.
Bonjour Etienne.
votre formule (tan20/260) n’est pas correct car en faisant ça, vous recherchez la tangente de (20/260) or 20/260, c’est DEJA la valeur de la tangente.
Je rappelle que tangente = Coté opposé / Coté Adjacent.
dans l’exemple ci dessus et si on considère le triangle rectangle du haut (celui ou il est écrit « l’angle de coupe » dans le dernier schema de l’article), le coté opposé vaut 250-230=20 et le coté adjacent vaut 260).
la tangente vaut donc 20/260 = 0.0770.
ça, c’est la valeur de la tangente, pas la valeur de l’angle.
Pour avoir la valeur de l’angle, il faut faire arctan(0.0770). Ce que l’on cherche, c’est l’arc (l’angle) dont la tangente vaut 0.0770.
sous Excel, puisque c’est ce que vous utilisez, la fonction s’écrit ATAN().
ATTENTION, en général, par défaut, Excel est en radian, pas en degré et donc ATAN(0.077) = 0.07677 (radians).
Pour avoir la valeur en degrés, il faut écrire DEGRES(ATAN(20/260))
(note : Pi radian = 180° donc pour passer des radians au degrés, il faut multiplier par 180/Pi)
A+