kW et kVA

Vous avez tous entendu ce terme de consommation électrique, les kWh (kilo watt heure).

Si vous laissez brancher un radiateur de 3000 watt pendant 1 heure de fonctionnement continu, c’est à dire que le radiateur chauffe en permanence sans atteindre la température de repos, la consommation sera de 3kWh.

Arrive cependant une particularité qui nécessite à mon avis une explication :

Parfois on lit kVA et à d’autres moments on lit kW.

On a vu dans la partie 3 que P = U x I, et P c’est des watts, alors pourquoi on écrit VA et pas W?

VA c’est bien Volt Ampère, donc c’est pareil, non ?

Oui et… non !

C’est vrai uniquement pour des appareils dit résistifs (qui chauffent), comme les radiateurs, les fours électriques à résistance (sans moteur), et les éclairages à filaments.

La formule véritablement complète de la puissance est (attention de ne pas vous étouffer) :

P = U x I x Cos Phi

Le cosinus Phi étant le coefficient de déphasage.

Ah, vadé rétro satanas, mais qu’a t-il dit ?

Comme le chantait si bien FGTH (Franky Goes To Hollywood) : « Relax » !

J’m’en vô vous conter simplemin l’histouor de c’treuc 😉 !

Il existe un élément très utilisé dans beaucoup d’appareils, c’est la bobine :

 

 

On en trouve principalement dans les moteurs.

C’est ce qu’on appelle les circuits inductifs.

Bien.

Sauf que les bobines, elles ont un comportement bien particulier, un comportement pour nous embobiner !

Ben dis donc… t’es en forme !

En effet, quand on fait passer un courant électrique dans un fil de cuivre enroulé sous la forme d’une bobine, cela crée un champ magnétique qui va s’opposer au passage du courant !

On dirait un truc qui se mord la queue, vous trouvez pas ?

Pour la petite histoire, cette particularité est connue sous la loi de Lenz-Faraday.

(Pour info : on dit que le passage du courant dans la bobine « induit » un champ magnétique, d’où le nom « inductances » donné aux bobines)

Ce comportement étrange de la bobine, c’est un peu comme vouloir remplir une bouteille avec de l’eau, mais que l’air expulsé dès le début du remplissage de la bouteille empêche l’eau de rentrer correctement dans la bouteille !

Ah ? Ça vous ai déjà arrivé 😉 ?

Retenez simplement qu’une bobine s’opposent aux variations du courant.

Rien de tel qu’un petit schéma pour comprendre le fonctionnement de la bobine (tout ça je vous le rappelle, c’est pour comprendre le foutu cos phi de la formule complète de la puissance !) :

 

 

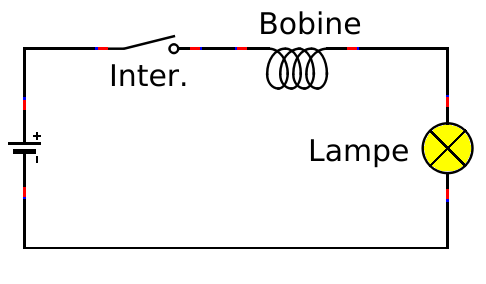
Et voici ce qu’il va se passer au niveau de la lampe :

 

 

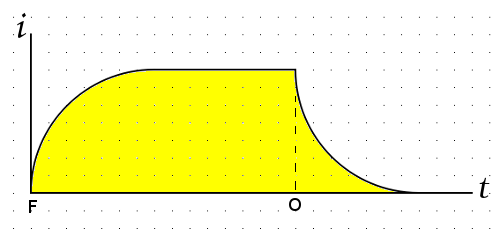
Explications :

i c’est le courant qui circule dans la lampe, t c’est le temps.

La couleur jaune correspond à l’allumage de l’ampoule.

A la fermeture (F) de l’interrupteur, la lampe ne s’allume pas car la bobine s’oppose momentanément au passage du courant 🙁 !

Quelques instants après, la lampe s’allume progressivement jusqu’à atteindre sa pleine luminosité.

A l’ouverture (O) de l’interrupteur, la tension d’alimentation s’arrête, mais la lampe reste éclairée et s’éteint progressivement.

Conclusion, on peut dire que la bobine est longue à la détente 🙂 !

Dans le jargon électrique, on dit que dans une bobine le courant est en retard sur la tension.

Ce retard s’appelle un déphasage.

 

NOTE :

Si vous avez encore une difficulté à comprendre ce qu’est la tension, un autre exemple est de considérer un ressort.

La tension du ressort s’exprime entre une extrémité fixe de ce ressort (par exemple un mur sur lequel il est accroché), et l’autre extrémité sur laquelle on tire pour tendre le ressort.

C’est la raison pour laquelle on parle souvent de différence de potentiel.

On compare toujours la tension entre 2 points différents.

« Normalement », la tension du ressort augmente proportionnellement à la traction appliquée.

Dans ce cas on dit que tension et traction sont en phases, c’est à dire qu’elles évoluent en même temps et dans le même sens.

La traction, elle, représente l’intensité i de l’électricité, le mouvement.

 

La bobine engendre un déphasage, mais un autre composant engendre aussi un déphasage (à l’opposé à la bobine), c’est le condensateur.

Le condensateur est d’ailleurs utilisé pour corriger les effets de la bobine.

Comment faire pour s’y retrouver entre les deux ?

Rien de plus simple.

Moi j’utilise le CURY et le SIRUS !

Ça va Totophe ???

Oui oui, c’est juste un truc de mémoire 🙂 :

C.U.R.I : Dans un Condensateur, U est en Retard sur I

SIRU : Dans une Self (le nom anglais d’une bobine), I est en Retard sur U

Pas bête, hein 🙂 ?

Vous avez je pense maintenant bien compris que le courant électrique correspond à de l’eau qui s’écoule.

Le condensateur a un fonctionnement parfaitement opposé à la bobine.

Un condensateur peut être assimilé à une toute petite batterie rechargeable.

C’est un réservoir vide au départ, donc n’ayant pas de niveau d’eau, il n’y a pas de potentiel, pas de différence de potentiel, pas de tension.

Quand je commence à remplir ce réservoir avec un courant d’eau, ce courant est bien présent avant qu’il n’y ait de l’eau dans le réservoir.

C’est logique.

La hauteur d’eau (la tension, la différence de potentiel) dans le réservoir (dans le condensateur), va augmenter progressivement.

La tension est bien en retard sur l’intensité.

Voilà pour le déphasage.

Ça va ?

 

Concernant la notion de cosinus, que vient faire le cosinus dans une formule d’électricité ?

Cela provient simplement du mode de production de l’électricité, généré par la rotation du champ magnétique d’un aimant à l’intérieur de bobinages :

 

 

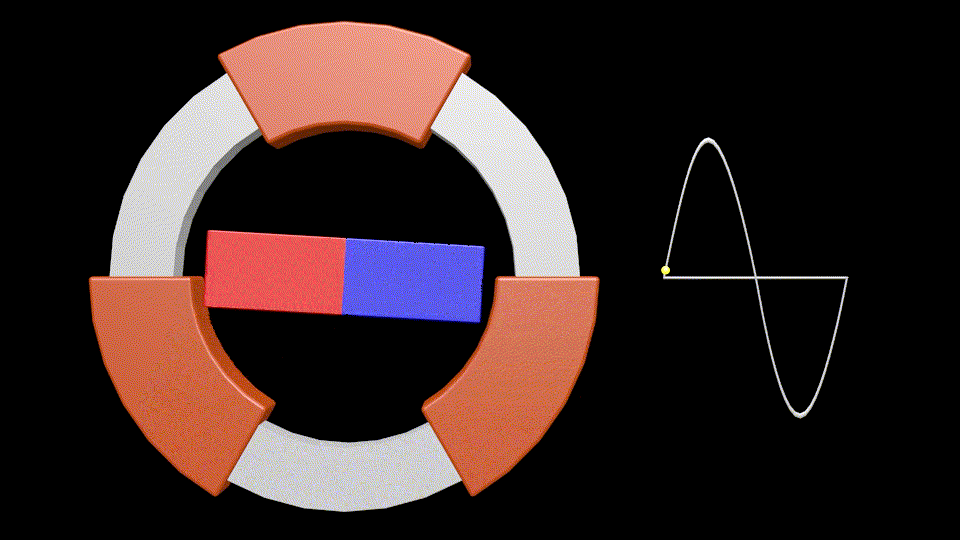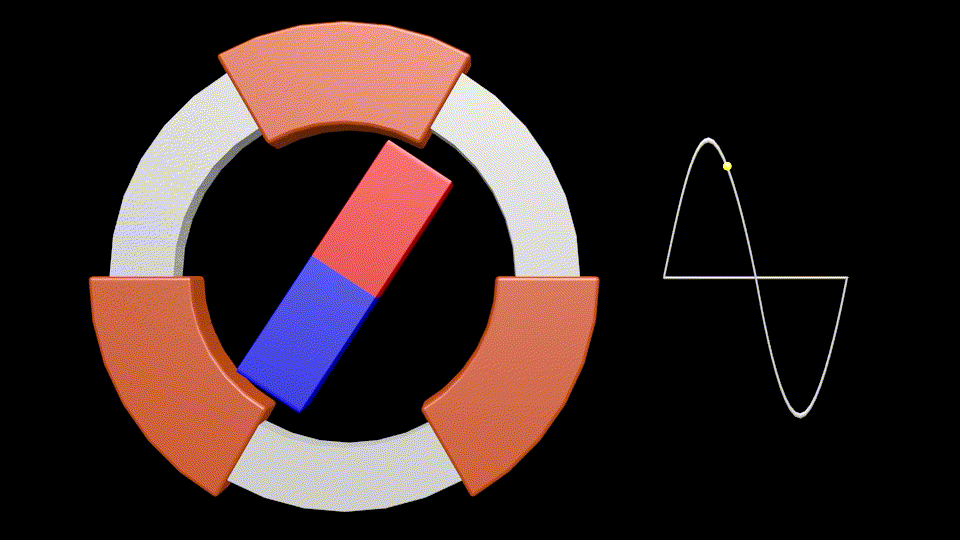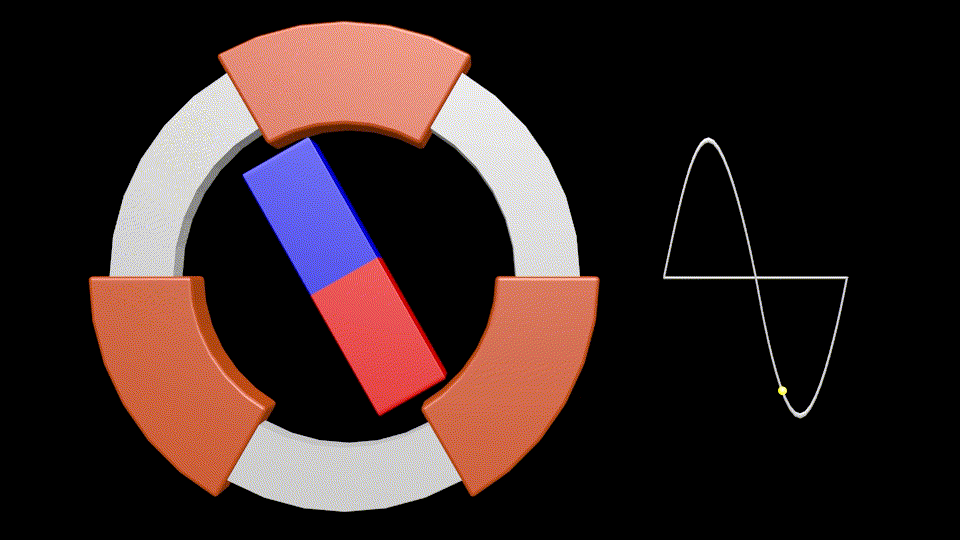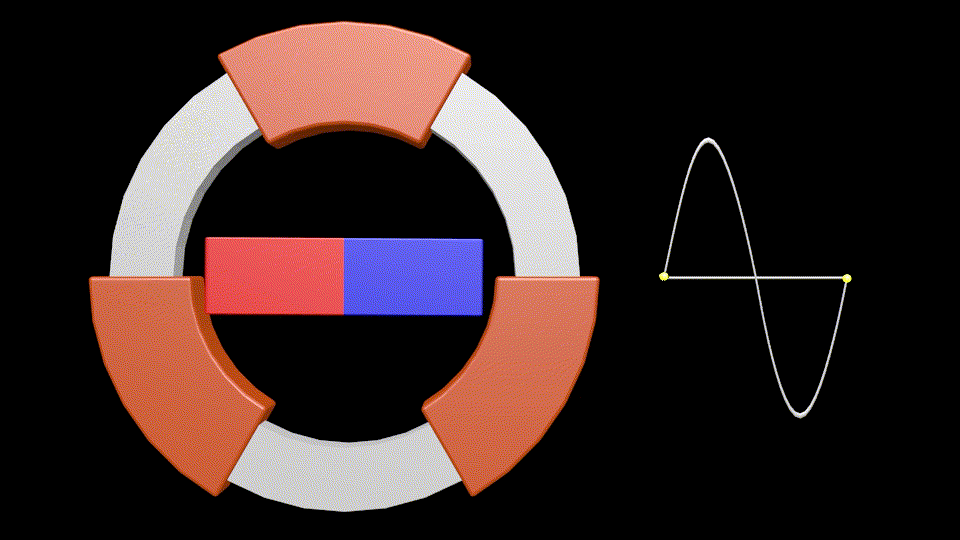
Sur cette animation il y a 3 bobinages réparties tous les 120°.

C’est le principe de « fabrication » du courant triphasé.

Il s’agit d’une animation très ralentie, car normalement la rotation s’effectue à 3000 trs/minute, afin d’obtenir la fréquence du réseau électrique de 50Hz, soit 50 cycles par seconde.

Nous y reviendrons plus loin.

Si l’on considère uniquement le bobinage supérieure, le côté rouge de l’aimant produisant un courant positif dans le bobinage et le bleu un courant négatif (choix arbitraire pour l’illustration), le point jaune à droite montre la variation du courant produit : la parfaite sinusoïde d’un courant alternatif mesurée au borne du bobinage supérieur.

L’aimant effectue une rotation complète pour produire un cycle complet (1 alternance positive et 1 alternance négative), soit 360°, d’où la trigonométrie 😉 !

Dans une simple résistance, qui est un élément passif, la tension et l’intensité restent en phase :

 

 

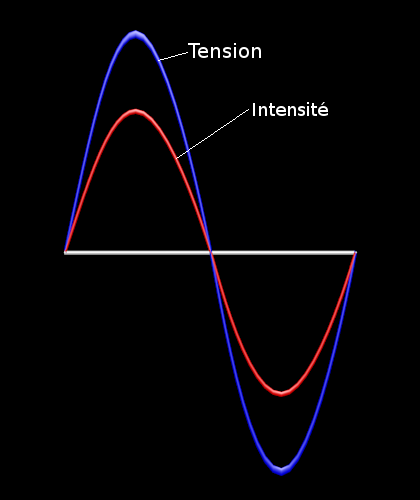
Les 2 grandeurs « travaillant » l’une et l’autre en phase, la puissance obtenue est maximum.

Dans un circuit inductif (avec des bobines), le courant est déphasé, I est en retard sur U :

 

 

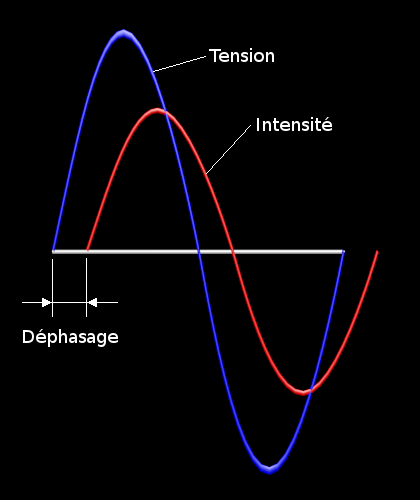
Les 2 grandeurs ne « travaillant » pas l’une et l’autre en phase, la puissance obtenue est réduite.

En effet, quand la tension est à son maximum, l’intensité ne l’est pas 🙁 !

Le coefficient de déphasage est appelé facteur de puissance ou cos Phi, et est une valeur comprise entre 0 et 1.

Pour ceux qui ne sont pas fan de trigonométrie, voici un rappel de ce que sont sinus et cosinus sur un cercle de rayon 1 :

 

 

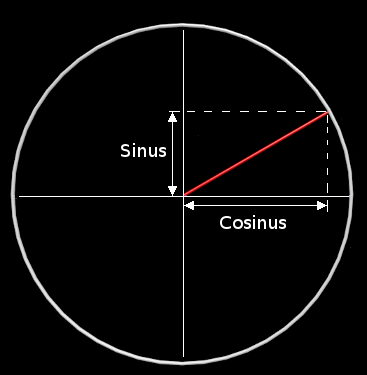
Donc, si je place sur ce cercle la tension et l’intensité d’une alimentation en phase, voici ce que l’on voit :

 

 

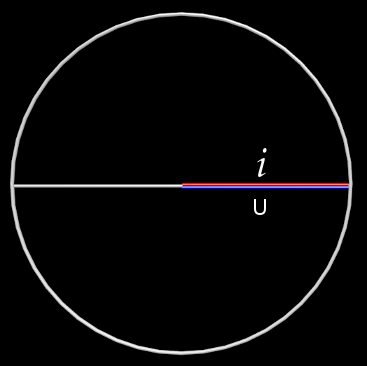
Explication :

Les 2 grandeurs sont en phases, donc varient en même temps (pour des besoins de compréhension, elles ont ici la même grandeur que le rayon du cercle).

Pas de déphasage signifie Phi = 0°, donc le cosinus de 0° = 1

Maintenant, s’il y a un déphasage dans un circuit à cause d’une inductance, voici ce que l’on voit (on tourne dans le sens des aiguilles d’une montre) :

 

 

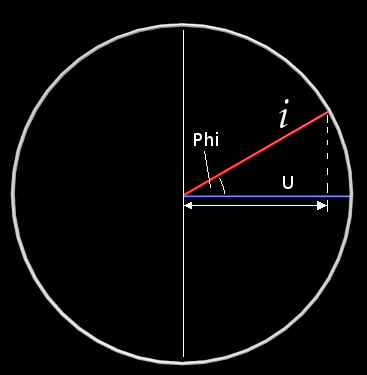
Explication :

Quand la tension U est maximum (à l’horizontal sur le dessin), l’intensité i est en retard à cause de l’angle Phi de déphasage.

Si à ce moment je veux calculer la puissance disponible, il me faut connaître sur le même « axe » que U la véritable valeur de i représentée par la double-flèche.

Et cette double-flèche, c’est le cos de l’angle Phi.

Quand il n’y a pas de déphasage, le cos Phi est égal à 1, et c’est la raison pour laquelle on peut simplifier que P = U x I.

Quand il y a déphasage, il est primordial d’utiliser la formule complète P = U x I x cos Phi.

 

Que se passe t-il dans la pratique ?

On a vu l’exemple de notre radiateur de 3000 W et qui consomme donc 13,04 A.

Si maintenant nous avons un autre appareil de 3000 W, mais qui présente un cos Phi de 0,8 à cause d’inductance dans sa conception.

P = U x I x 0,8

P = 230 x 13,04 x 0,8

P = 2400 W

Aïe ! Ça ne va pas du tout 🙁 !

L’appareil a besoin de 3000 W pour fonctionner, et là on ne lui donne que 2400 W.

Que va t-il faire alors ?

Pour atteindre ses 3000 W de fonctionnement, comme la tension est toujours 230 V, il va demander plus de courant sur le réseau 🙁 !

D’où une augmentation de la consommation et une facture qui grimpe !

Heureusement, les fabricants utilisent des condensateurs dans les appareils inductifs pour corriger un mauvais cos Phi.

Vous n’avez donc normalement rien à faire.

Sauf vous assurer de dérouler entièrement votre rallonge de 25m à enrouleur même si vous n’en utilisez que 2 mètres !

Parce qu’en laissant le reste dans l’enrouleur, vous créez une bobine, donc un déphasage, et un cos Phi qui va s’occuper de faire grimper votre consommation !

 

Que faut -il retenir :

Le déphasage est la raison de la distinction en kVA et kW.

Comme on ne peut savoir exactement quels appareils vont être branchés sur le réseau, on ne peut qu’estimer une puissance fournie idéale et sans déphasage, donc en kVA.

Par contre, avec le compteur, on connaît la consommation réelle occasionnée indifféremment avec ou sans déphasage, et là on l’exprime en kW !

C’est aussi « simple » que ça !